|
С.И. Головань, М.А. Спиридонов
Бизнес-планирование и инвестирование
Учебник. Ростов н/Д: Феникс, 2008. – 302 с.
9. МЕТОДЫ ОЦЕНКИ ЭФФЕКТИВНОСТИ ИНВЕСТИЦИОННЫХ ПРОЕКТОВ
9.3 Методы оценки эффективности инвестиций
9.3.6 Метод внутренней нормы прибыли проекта (IRR, ВНД)
Внутренняя норма прибыли
(внутренняя норма доходности) – обычно это такое положительное число R, что при норме дисконта r = R NPV
проекта обращается в 0.
Таким образом, чтобы найти
значение внутренней нормы прибыли проекта, необходимо решить уравнение вида 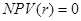 относительно r. относительно r.
Экономический смысл показателя IRR
при анализе эффективности инвестиций заключается в следующем: внутренняя норма
доходности показывает максимально допустимый относительный уровень расходов,
которые могут быть ассоциированы с данным проектом. Например, если проект
полностью финансируется за счет кредита коммерческого банка, то значение IRR
показывает верхнюю границу допустимого уровня банковской процентной ставки,
превышение которого делает проект убыточным.
Для оценки эффективности проекта
значение IRR необходимо сопоставить с нормой
дисконта r. Проекты, у которых 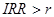 , имеют положительное NPV и поэтому эффективны. А те, которых , имеют положительное NPV и поэтому эффективны. А те, которых 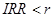 , имеют отрицательное NPV и поэтому неэффективны. , имеют отрицательное NPV и поэтому неэффективны.
IRR
может быть использована также для:
-
оценки эффективности проекта, если известны приемлемые значения IRR (зависящие от области применения) у проектов
различного типа;
-
оценки степени устойчивости проекта (по разности  ); );
-
установления участниками проекта нормы дисконта r
по данным об IRR альтернативных направлений
вложения ими собственных средств.
На практике расчет IRR удобнее всего вести с помощью компьютерных программ,
т. е. путем перебора значений r
определить R, при которой NPV обращается в 0.
Приближенное значение IRR можно получить путем расчета методом
интерполяции. Для расчета необходимо два значения NPV,
наиболее близко лежащие к нулю: одно – минимальное положительное значение,
второе – максимальное отрицательное значение, а также соответствующие каждому
из NPV нормы дисконта:
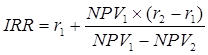 (9.10) (9.10)
где 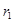 –
норма дисконта, при которой NPV> 0; –
норма дисконта, при которой NPV> 0;
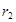 – норма дисконта, при которой NPV<
0; – норма дисконта, при которой NPV<
0;
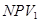 – положительное значение NPV при норме дисконта – положительное значение NPV при норме дисконта 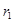 ; ;
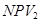 – отрицательное значение NPV при норме дисконта – отрицательное значение NPV при норме дисконта 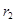 . .
Недостатком метода IRR является то, что уравнение 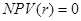 необязательно имеет один
положительный корень. Оно может вообще не иметь корней (1) или иметь несколько
положительных корней (2) (см. рис. 9.2). необязательно имеет один
положительный корень. Оно может вообще не иметь корней (1) или иметь несколько
положительных корней (2) (см. рис. 9.2).
Для того, чтобы преодолеть эти
трудности, лучше определять IRR иначе:
|
IRR
– это положительное число R такое, что NPV:
-
при норме дисконта 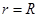 обращается в
0; обращается в
0;
-
при всех 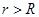 отрицательна; отрицательна;
-
при всех 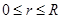 положительна. положительна.
|
Определенная таким образом IRR, если только существует, всегда единственна. В
частности, для проекта, приведенного на рисунке 9.2, IRR
отсутствует.[3]
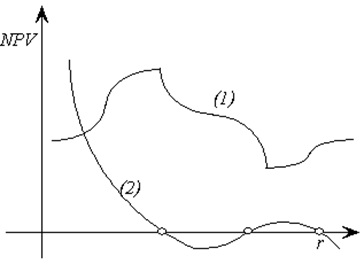
Рис.
9.2 Зависимость NPV от
нормы дисконта
Другим недостатком метода
IRR, является то, что различные ряды денежного
потока могут создавать одинаковую IRR. Кроме
того, он может противоречить результатам метода NPV.
(см. рис. 9.3)
IRR
проекта Б (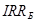 ) выше, чем ) выше, чем 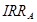 ,
и для любой нормы дисконта (r) между ,
и для любой нормы дисконта (r) между 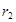 и IRR и IRR 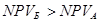 . Если
минимальный коэффициент окупаемости меньше . Если
минимальный коэффициент окупаемости меньше 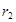 ,
тогда оба проекта будут все еще приемлемы с точки зрения прибыльности. Однако в
этом случае приоритет должен быть отдан проекту А, если на выбор проекта
доминирующее влияние оказывает NPV. ,
тогда оба проекта будут все еще приемлемы с точки зрения прибыльности. Однако в
этом случае приоритет должен быть отдан проекту А, если на выбор проекта
доминирующее влияние оказывает NPV.
Норма дисконта, при которой NPV обоих проектов одинаков, называется нормой
пересечения (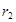 ). ).
При достаточно абстрактных
условиях совершенно одинаковых проектных рисков, одинаковых сроков жизни и
сравнимых размеров инвестиций, проект с более высоким доходом обычно получает
приоритет.
Особенно осторожно следует
использовать метод IRR для оценки взаимоисключающих
проектов, так как в случае с такими проектами речь идет не об отклонении /
принятии, а о принятии одного проекта из двух и более (застройка участка).
Применяя критерий IRR следует выбрать проект Б, а при использовании
критерия NPV решение зависит от применяемой
нормы дисконта. Например, на рис. 9.3 показано, что если возможная стоимость
капитала соответствует 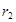 , то у обоих проектов
будет одинаковая NPV (отрезок
К-Д). Если стоимость капитала меньше, то может быть выбран проект А (отрезок
И-Г). Если ставка дисконта больше , то у обоих проектов
будет одинаковая NPV (отрезок
К-Д). Если стоимость капитала меньше, то может быть выбран проект А (отрезок
И-Г). Если ставка дисконта больше 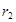 , выбор будет
сделан в пользу проекта Б (отрезок Л-Ж). , выбор будет
сделан в пользу проекта Б (отрезок Л-Ж).
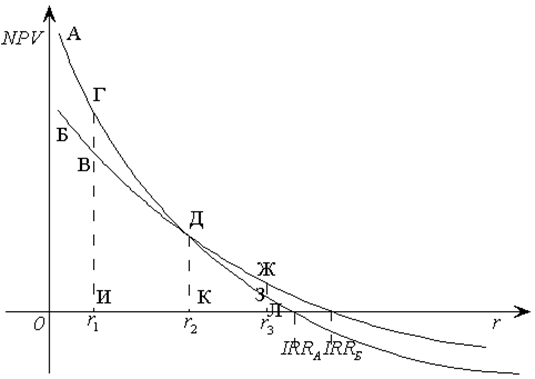
Рис.
9.3 NPV, IRR и ранжирование проектов
Итак, из трех сложных методов
оценки (за исключением DPP):
-
метод NPV позволяет оценить ожидаемые
накопленные чистые прибыли на инвестиции, дисконтированные к настоящему
моменту;
-
индекс рентабельности показывает накопленную чистую прибыль, созданную
единицей вложенного капитала;
-
IRR показывает чистый доход (т.е.
прибыль), выраженный как норма прибыльности в год, однако не позволяя при этом
сделать какой-либо вывод относительно накопленных прибылей.
В качестве резюме обозначим условия
эффективности инвестиционных проектов – для того, чтобы проект были признан
эффективным, необходимо выполнение какого-нибудь из следующих условий:
1) 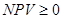 ; ;
2) про критерию IRR 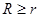 , при условии, что R – единственный положительный корень уравнения , при условии, что R – единственный положительный корень уравнения 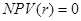 ; ;
3) 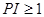 ; ;
4) 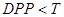 . .
При этом, если выполнено условие
2, остальные условия также будут выполняться, если же выполнено любое из
условий 1, 3, 4, то будут выполнены и другие из этих условий (хотя IRR проекта может и не существовать).
[3]
Виленский П. Л., Лившиц В. Н., Орлова Е. Р., Смоляк С. Л. Оценка эффективности
инвестиционных проектов. Учебно-практическое пособие. - М.: Дело, 1998. С. 57.
|

